GitHub

Transformations

In tensor network computations, it is good practice to apply various transformations to simplify the network structure, reduce computational cost, or prepare the network for further operations. These transformations modify the network's structure locally by permuting, contracting, factoring or truncating tensors.

A crucial reason why these methods are indispensable lies in their ability to drastically reduce the problem size of the contraction path search and also the contraction. This doesn't necessarily involve reducing the maximum rank of the Tensor Network itself, but more importantly, it reduces the size (or rank) of the involved tensors.

Our approach is based in (Gray and Kourtis, 2021), which can also be found in quimb.

In Tenet, we provide a set of predefined transformations which you can apply to your TensorNetwork using both the transform/transform! functions.

Tenet.transform — Function
transform(tn::TensorNetwork, config::Transformation)
transform(tn::TensorNetwork, configs)

Return a new TensorNetwork where some Transformation has been performed into it.

See also: transform!.

source
Tenet.transform! — Function
transform!(tn::TensorNetwork, config::Transformation)
transform!(tn::TensorNetwork, configs)

In-place version of transform.

source

Available transformations

Hyperindex converter

Tenet.HyperFlatten — Type
HyperFlatten <: Transformation

Convert hyperindices to COPY-tensors, represented by DeltaArrays. This transformation is always used by default when visualizing a TensorNetwork with plot.

See also: HyperGroup.

source

Contraction simplification

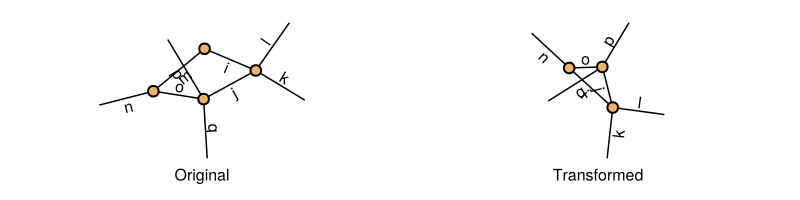
Example block output

Diagonal reduction

Tenet.DiagonalReduction — Type
DiagonalReduction <: Transformation

Reduce the dimension of a Tensor in a TensorNetwork when it has a pair of indices that fulfil a diagonal structure.

Keyword Arguments

  • atol Absolute tolerance. Defaults to 1e-12.
source
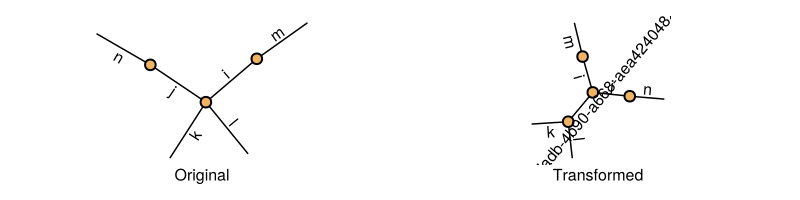
Example block output

Anti-diagonal reduction

Tenet.AntiDiagonalGauging — Type
AntiDiagonalGauging <: Transformation

Reverse the order of tensor indices that fulfill the anti-diagonal condition. While this transformation doesn't directly enhance computational efficiency, it sets up the TensorNetwork for other operations that do.

Keyword Arguments

  • atol Absolute tolerance. Defaults to 1e-12.
  • skip List of indices to skip. Defaults to [].
source

Dimension truncation

Tenet.Truncate — Type
Truncate <: Transformation

Truncate the dimension of a Tensor in a TensorNetwork when it contains columns with all elements smaller than atol.

Keyword Arguments

  • atol Absolute tolerance. Defaults to 1e-12.
  • skip List of indices to skip. Defaults to [].
source
Example block output

Split simplification

Tenet.SplitSimplification — Type
SplitSimplification <: Transformation

Reduce the rank of tensors in the TensorNetwork by decomposing them using the Singular Value Decomposition (SVD). Tensors whose factorization do not increase the maximum rank of the network are left decomposed.

Keyword Arguments

  • atol Absolute tolerance. Defaults to 1e-10.
source
Example block output