The Quantum class

The Site type

A Site is a helper type for representing sites.

julia> Site(1)
1

julia> site"1"
1

Sites can refer to multi-dimensional cartesian indices too:

julia> Site(4,3)
(4, 3)

julia> site"4,3"
(4, 3)

By default, a Site refers to a normal physical, output or covariant index. If you want to create a dual physical, input or contravariant index, you can pass the dual=true kwarg to the constructor or just call adjoint on it.

julia> Site(5; dual=true)
5'

julia> Site(5)'
5'

julia> adjoint(Site(5))
5'

julia> site"5'"
5'

Warning

We recommend the use of the @site_str macro (i.e. the site"..." expression) instead of the Site constructor, but the only caveat is it cannot interpolate variables yet. For now, use it only in cases where you can hardcode the site like in the REPL or scripts. Check out the tracking issue fo#274 for more information.

The Quantum type

A Quantum is just a TensorNetwork with a mapping between indices and Sites. It implements the AbstractQuantum interface so any subtype of AbstractQuantum can access to its features.

julia> tn = TensorNetwork([Tensor(zeros(2,2,2), [:p1,:i,:k]), Tensor(zeros(2,2,2), [:p2,:i,:j]), Tensor(zeros(2,2,2), [:p3,:j,:k])])
TensorNetwork (#tensors=3, #inds=6)

julia> qtn = Quantum(tn, Dict([site"1" => :p1, site"2" => :p2, site"3" => :p3]))
Quantum (inputs=0, outputs=3)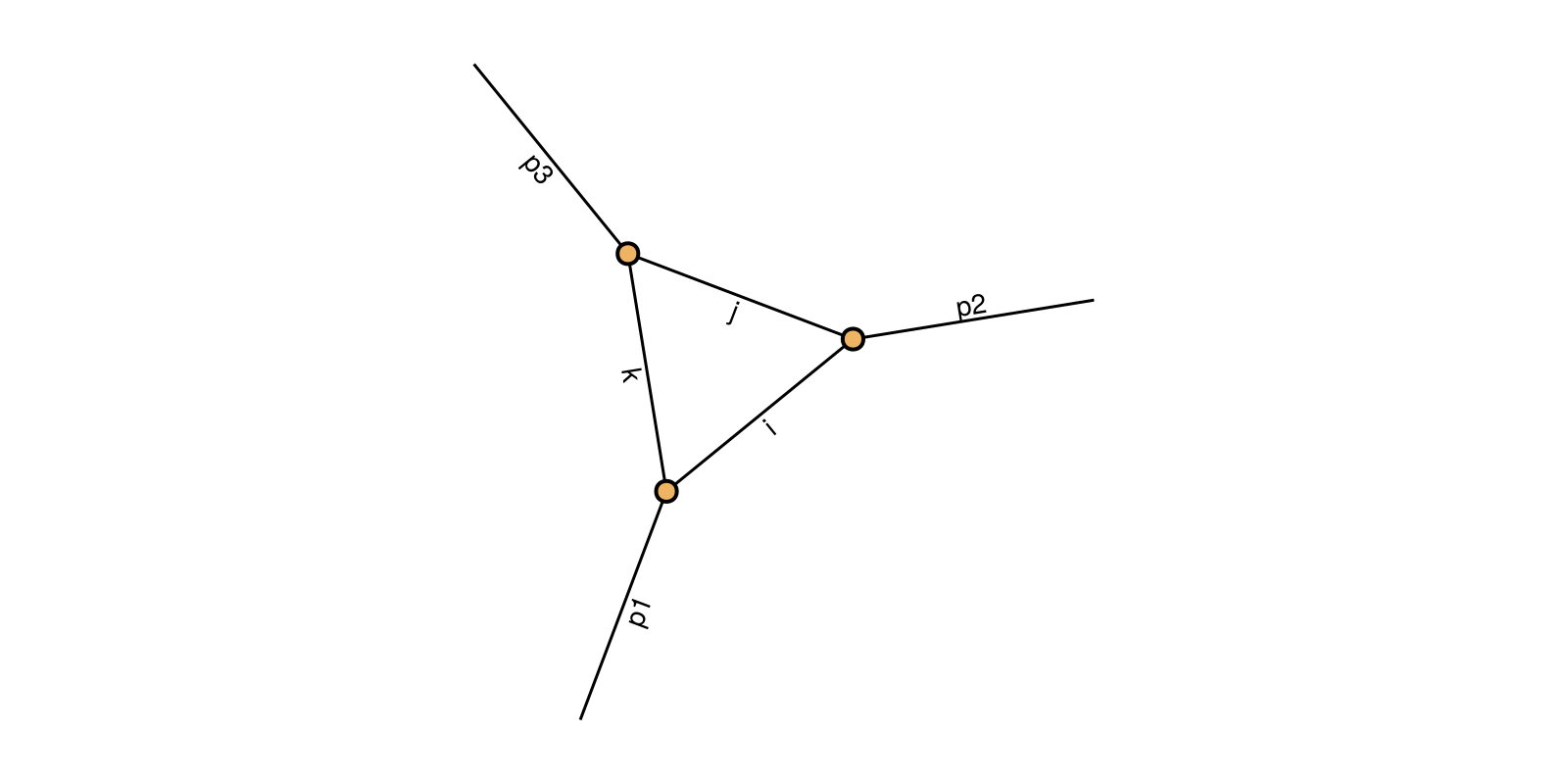

Note that Quantum implements the AbstractTensorNetwork contract, so it inherits all the functionality of TensorNetwork!

julia> :i ∈ qtn
true

julia> tensors(qtn; contains=:p1) .|> inds
1-element Vector{Tuple{Symbol, Symbol, Symbol}}:
 (:p1, :i, :k)

Quantum provides a new function sites, which returns the

julia> sites(qtn)
3-element Vector{Site}:
 1
 2
 3

Just like tensors and inds, it has some kwarg-dispatched methods.

julia> sites(qtn; set=:inputs)
Site[]

julia> sites(qtn; set=:outputs)
3-element Vector{Site}:
 1
 2
 3

julia> sites(qtn; at=:p2)
2

Speaking of which, Quantum also extends tensors and inds with new kwarg-methods:

julia> tensors(qtn; at=site"1")
2×2×2 Tensor{Float64, 3, Array{Float64, 3}}:
[:, :, 1] =
 0.0  0.0
 0.0  0.0

[:, :, 2] =
 0.0  0.0
 0.0  0.0

julia> inds(qtn; at=site"1")
:p1

julia> inds(qtn; set=:physical)
3-element Vector{Symbol}:
 :p1
 :p2
 :p3

julia> inds(qtn; set=:virtual)
3-element Vector{Symbol}:
 :k
 :j
 :i

julia> inds(qtn; set=:inputs)
Symbol[]

julia> inds(qtn; set=:outputs)
3-element Vector{Symbol}:
 :p1
 :p2
 :p3

Note

In Tenet, an open index ≠ a physical index. Physical indices are the ones used to connect and interact with other states or operators, and are only the ones marked with Sites in Quantum. Open indices not marked as physical are still virtual indices and can be later used to coomplement with other Quantum; e.g. like a quantum state purification.

Connectivity

The whole point of Quantum is to be able to connect TensorNetworks without requiring the user to manually match the indices. Quantum automatically takes care of matching input-output Sites, renaming the indices accordingly and finally connecting all tensors into one Quantum Tensor Network.

For example, the following expectation value...

$$⟨\psi \mid O\mid \psi ⟩$$

...can be expressed in Tenet as:

exp_val = merge(ψ, O, ψ')

Warning

Unlike linear algebra notation, in which time evolution goes from right-to-left, merge and merge! go from left-to-right to keep consistency with Julia semantics. This is not such a big deal as you can imagine: quantum circuits are drawn from left-to-right and there are Tensor Networks pictures in the literature where time goes down-to-up and up-to-down!

Note that adjoint and adjoint! just conjugate the tensors and switch the Sites from normal to dual (output to input) and viceversa.

The Socket trait

Depending on the number of inputs and outputs, a [Quantum] can be a state, a dual state or an operator. You can use the socket function to find out of which type it is your [Quantum] object:

julia> socket(ψ)
Tenet.State(false)

julia> socket(ψ')
Tenet.State(true)

julia> socket(O)
Tenet.Operator()

julia> socket(exp_val)
Tenet.Scalar()

socket is a dynamic trait: it returns an object whose type represents a property of the Quantum object, which in this case represents whether the Quantum object is a State (has information about being a normal or dual state), an Operator or a Scalar (a Tensor Network with no physical indices).

The motivation to use traits is that depending on the trait value, methods can dispatch to more specialized methods; i.e. you have a method optimized for State and another method optimized for Operator for instance. You can read more about it in Interfaces and Traits.

DocumenterMermaid.MermaidScriptBlock([...])