The TensorNetwork class

In Tenet, Tensor Networks are represented by the TensorNetwork type. In order to fit all posible use-cases of TensorNetwork implements a hypergraph^[1] of Tensor objects, with support for open-indices and multiple shared indices between two tensors.

For example, this Tensor Network...

... can be constructed as follows:

julia> tn = TensorNetwork([
           Tensor(zeros(2,2), (:i, :m)), # A
           Tensor(zeros(2,2,2), (:i, :j, :p)), # B
           Tensor(zeros(2,2,2), (:n, :j, :k)), # C
           Tensor(zeros(2,2,2), (:p, :k, :l)), # D
           Tensor(zeros(2,2,2), (:m, :n, :o)), # E
           Tensor(zeros(2,2), (:o, :l)), # F
       ])
TensorNetwork (#tensors=6, #inds=8)

Tensors can be added or removed after construction using push!, pop!, delete! and append! methods.

julia> A = only(pop!(tn, [:i, :m]))
2×2 Tensor{Float64, 2, Matrix{Float64}}:
 0.0  0.0
 0.0  0.0

julia> tn
TensorNetwork (#tensors=5, #inds=8)

julia> push!(tn, A)
TensorNetwork (#tensors=6, #inds=8)

You can also replace existing tensors and indices with replace and replace!.

julia> :i ∈ tn
true

julia> replace!(tn, :i => :my_index)
TensorNetwork (#tensors=6, #inds=8)

julia> :i ∈ tn
false

julia> :my_index ∈ tn
true

Warning

Note that although it is a bit unusual but completely legal to have more than one tensor with the same indices, there can be problems when deciding which tensor to be replaced. Because of that, you must pass the exact tensor you want to replace. A copy of it won't be valid.

The AbstractTensorNetwork interface

Subclasses of TensorNetwork inherit from the AbstractTensorNetwork abstract type. Subtypes of it are required to implement a TensorNetwork method that returns the composed TensorNetwork object. In exchange, AbstracTensorNetwork automatically implements tensors and inds methods for any interface-fulfilling subtype.

As the names suggest, tensors returns tensors and inds returns indices.

julia> tensors(tn)
6-element Vector{Tensor}:
 [0.0 0.0; 0.0 0.0;;; 0.0 0.0; 0.0 0.0]
 [0.0 0.0; 0.0 0.0]
 [0.0 0.0; 0.0 0.0;;; 0.0 0.0; 0.0 0.0]
 [0.0 0.0; 0.0 0.0;;; 0.0 0.0; 0.0 0.0]
 [0.0 0.0; 0.0 0.0]
 [0.0 0.0; 0.0 0.0;;; 0.0 0.0; 0.0 0.0]

julia> inds(tn)
8-element Vector{Symbol}:
 :l
 :m
 :o
 :p
 :n
 :j
 :k
 :i

What is interesting about them is that they implement a small query system based on keyword dispatching. For example, you can get the tensors that contain or intersect with a subset of indices using the contains or intersects keyword arguments:

Note

Keyword dispatching doesn't work with multiple unrelated keywords. Checkout Keyword dispatch for more information.

julia> tensors(tn; contains=[:i,:m]) # A
1-element Vector{Tensor}:
 [0.0 0.0; 0.0 0.0]

julia> tensors(tn; intersects=[:i,:m]) # A, B, E
3-element Vector{Tensor}:
 [0.0 0.0; 0.0 0.0;;; 0.0 0.0; 0.0 0.0]
 [0.0 0.0; 0.0 0.0]
 [0.0 0.0; 0.0 0.0;;; 0.0 0.0; 0.0 0.0]

Or get the list of open indices (which in this case is none):

julia> inds(tn; set = :open)
Symbol[]

The list of available keywords depends on the layer, so don't forget to check the 🧭 API reference!

Contraction

When contracting two tensors in a Tensor Network, diagrammatically it is equivalent to fusing the two vertices of the involved tensors.

Matrix Multiplication using Tensor Network notation

The ultimate goal of Tensor Networks is to compose tensor contractions until you get the final result tensor. Tensor contraction is associative, so mathematically the order in which you perform the contractions doesn't matter, but the computational cost depends (and a lot) on the order (which is also known as contractio path). Actually, finding the optimal contraction path is a NP-complete problem and general tensor network contraction is #P-complete.

But don't fear! Optimal contraction paths can be found for small tensor networks (i.e. in the order of of up to 40 indices) in a laptop, and several approximate algorithms are known for obtaining quasi-optimal contraction paths. In Tenet, contraction path optimization is delegated to the EinExprs library. A EinExpr is a lower-level form of a Tensor Network, in which the contents of the arrays have been left out and the contraction path has been laid out as a tree. It is similar to a symbolic expression (i.e. Expr) but in which every node represents an Einstein summation expression (aka einsum). You can get the EinExpr (which again, represents the contraction path) by calling einexpr.

julia> path = einexpr(tn; optimizer=Exhaustive())
Symbol[] 4 flops, 1 elems
├─ [:l, :o] 0 flops, 4 elems
└─ [:l, :o] 16 flops, 4 elems
   ├─ [:i, :n, :o] 16 flops, 8 elems
   │  ├─ [:i, :m] 0 flops, 4 elems
   │  └─ [:m, :n, :o] 0 flops, 8 elems
   └─ [:i, :n, :l] 32 flops, 8 elems
      ├─ [:p, :k, :l] 0 flops, 8 elems
      └─ [:i, :p, :n, :k] 32 flops, 16 elems
         ├─ [:i, :j, :p] 0 flops, 8 elems
         └─ [:j, :n, :k] 0 flops, 8 elems

Once a contraction path is found, you can pass it to the contract method. Note that if no contraction path is provided, then Tenet will choose an optimizer based on the characteristics of the Tensor Network which will be used for finding the contraction path.

julia> contract(tn; path=path)
0-dimensional Tensor{Float64, 0, Array{Float64, 0}}:
0.0

julia> contract(tn)
0-dimensional Tensor{Float64, 0, Array{Float64, 0}}:
0.0

If you want to manually perform the contractions, then you can indicate which index to contract by just passing the index. If you call contract!, the Tensor Network will be modified in-place and if contract is called, a mutated copy will be returned.

julia> contract(tn, :i)
TensorNetwork (#tensors=5, #inds=7)

Visualization

Tenet provides visualization support with GraphMakie. Import a Makie backend and call GraphMakie.graphplot on a TensorNetwork.

graphplot(tn, layout=Stress(), labels=true)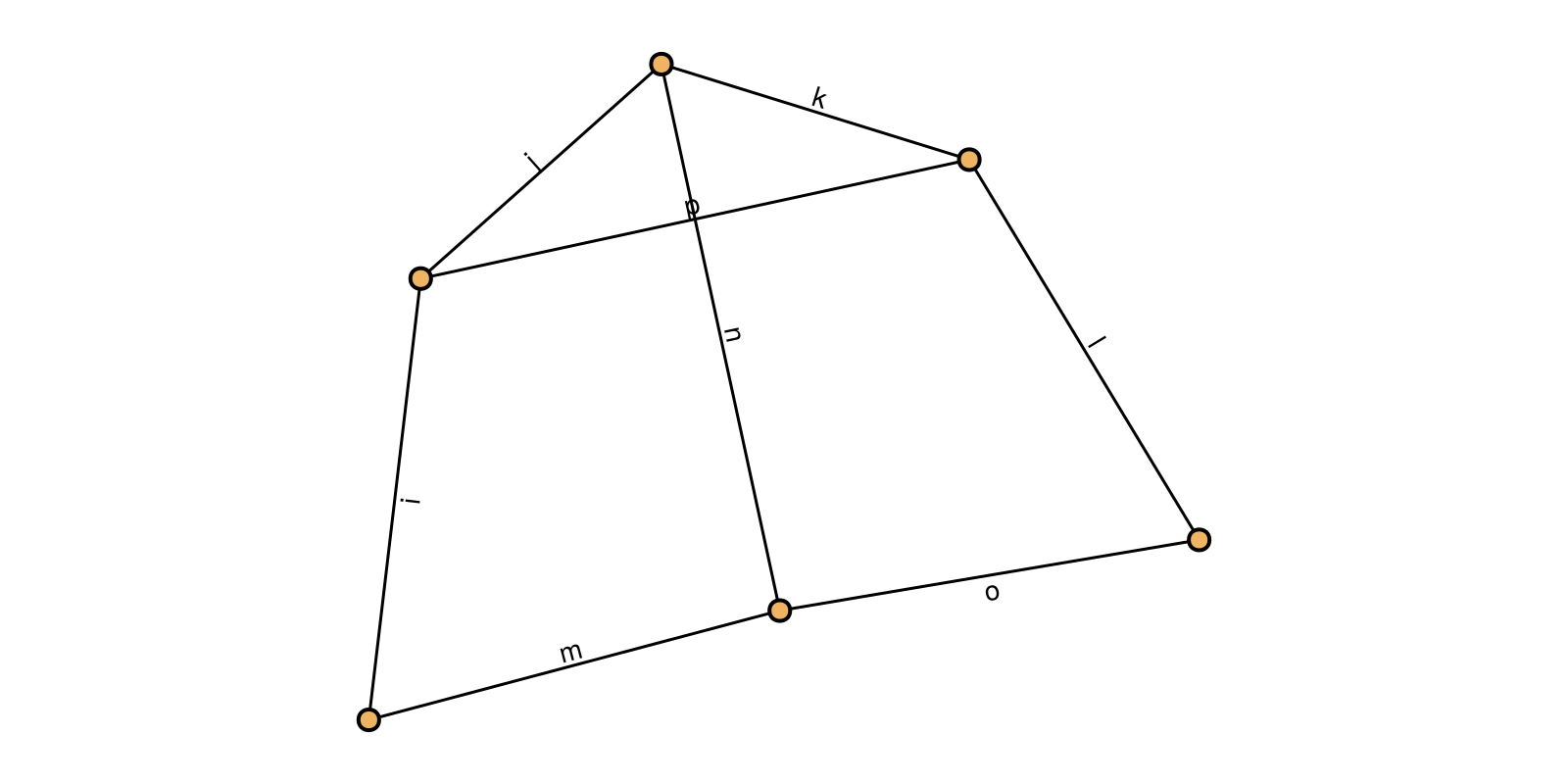

Transformations

In Tensor Network computations, it is good practice transform before in order to prepare the network for further operations. In the case of exact Tensor Network contraction, a crucial reason why these methods are indispensable lies in their ability to drastically reduce the problem size of the contraction path search. This doesn't necessarily involve reducing the maximum rank of the Tensor Network itself (althoug it can), but more importantly, it reduces the size of the (hyper)graph. These transformations can modify the network's structure locally by permuting, contracting, factoring or truncating tensors. Our approach is based in (Gray and Kourtis, 2021), which can also be found in quimb.

Tenet provides a set of predefined transformations which you can apply to your TensorNetwork using the transform/transform! functions.

HyperFlatten

The HyperFlatten transformation converts hyperindices to COPY-tensors (i.e. Kronecker deltas). It is useful when some method requires the Tensor Network to be represented as a graph and not as a hypergraph. The opposite transformation is HyperGroup.

fig = Figure() # hide

A = Tensor(rand(2,2), [:i,:j])
B = Tensor(rand(2,2), [:i,:k])
C = Tensor(rand(2,2), [:i,:l])

tn = TensorNetwork([A, B, C])
transformed = transform(tn, Tenet.HyperFlatten())

graphplot!(fig[1, 1], tn; layout=Stress(), labels=true) #hide
graphplot!(fig[1, 2], transformed; layout=Stress(), labels=true) #hide

Label(fig[1, 1, Bottom()], "Original") #hide
Label(fig[1, 2, Bottom()], "Transformed") #hide

fig #hide

Contraction simplification

The ContractionSimplification transformation contracts greedily tensors whose resulting tensor is smaller (in number of elements or in rank, it's configurable). These preemptive contractions don't affect the result of the contraction path but reduce the search space.

A = Tensor(rand(2, 2, 2, 2), (:i, :j, :k, :l))
B = Tensor(rand(2, 2), (:i, :m))
C = Tensor(rand(2, 2, 2), (:m, :n, :o))
E = Tensor(rand(2, 2, 2), (:o, :p, :j))

tn = TensorNetwork([A, B, C, E])
transformed = transform(tn, Tenet.ContractSimplification)

Diagonal reduction

The DiagonalReduction transformation tries to reduce the rank of tensors by looking up tensors that have pairs of indices with a diagonal structure between them.

$$A_{ijkl}=\{\begin{array}{ll}{A}_{ikl}^{\prime }& \text{for }i=j\\ 0& \text{for }i\ne j\end{array}\mapsto A_{ijkl}=A_{\alpha kl}^{\prime }{\delta }_{\alpha ij}$$

In such cases, the diagonal structure between the indices can be extracted into a COPY-tensor and the two indices of the tensor are fused into one.

data = zeros(Float64, 2, 2, 2, 2)
for i in 1:2
    for j in 1:2
        for k in 1:2
            data[i, i, j, k] = k
        end
    end
end

A = Tensor(data, (:i, :j, :k, :l))

tn = TensorNetwork([A])
transformed = transform(tn, Tenet.DiagonalReduction)

Truncation

The Truncate transformation truncates the dimension of a Tensor if it founds slices of it where all elements are smaller than a given threshold.

data = rand(3, 3, 3)
data[:, 1:2, :] .= 0

A = Tensor(data, (:i, :j, :k))
B = Tensor(rand(3, 3), (:j, :l))
C = Tensor(rand(3, 3), (:l, :m))

tn = TensorNetwork([A, B, C])
transformed = transform(tn, Tenet.Truncate)

Split simplification

The SplitSimplification transformation decomposes a Tensor using the Singular Value Decomposition (SVD) if the rank of the decomposition is smaller than the original; i.e. there are singular values which can be truncated.

# outer product has rank=1
v1 = Tensor([1, 2, 3], (:i,))
v2 = Tensor([4, 5, 6], (:j,))
t1 = contract(v1, v2)

m1 = Tensor(rand(3, 3), (:k, :l))
tensor = contract(t1, m1)

tn = TensorNetwork([
    tensor,
    Tensor(rand(3, 3, 3), (:k, :m, :n)),
    Tensor(rand(3, 3, 3), (:l, :n, :o))
])
transformed = transform(tn, Tenet.SplitSimplification)

DocumenterMermaid.MermaidScriptBlock([...])

---

1. A hypergraph is the generalization of a graph but where edges are not restricted to connect 2 vertices, but any number of vertices. ↩︎